A Schrödinger equation associated with a Schrödinger operator $ H$ can be used to model how well quantum wave packets travel in a quasicrystal—see [Damanik and Tcheremchantsev2010] for details. A key step in the determination of the large time behaviour of solutions to this equation is the understanding of the properties of the spectrum of $ H$ and of the corresponding spectrum measures. Theorem 2.1.1 below illustrates the kind of properties that are of interest. Before stating it, we introduce some notation and some definitions.

Given a finite alphabet $ \mathcal{A}$, let $ \boldsymbol{x}\in\mathcal{A}^\Naa$ (resp. $ \boldsymbol{x}\in\mathcal{A}^\Zaa$) be a single sided (resp. a double sided) recurrent sequence over $ \mathcal{A}$. The complexity of $ \boldsymbol{x}$ is defined for each integer $ n\ge 1$ as \begin{eqnarray*} p(n):=\#\left\{x_m\dots x_{m+n-1}\, : \, m\in\Zaa \right\} \end{eqnarray*} if the sequence is double sided. If it is single sided, the complexity is defined in the same way upon restricting $ m$ to the set of positive integers. When $ \boldsymbol{x}$ is aperiodic (i.e. not ultimately periodic), it is easily seen that $ p(n)\ge n+1$ for all $ n\ge 1$. The sequence $ \boldsymbol{x}$ is Sturmian if it is aperiodic and if it has minimal complexity; that is, if $ p(n)= n+1$ for all $ n\ge 1$. This definition implies that the alphabet defining a Sturmian sequence contains exactly two letters which may be denoted without loss of generality by 0 and 1. One can then show ([Lothaire2002]) that a double sided (resp. single sided) Sturmian sequence is exactly of one of the following forms: for all $ m\in\Zaa$ (resp. for all $ m\in\Naa$), \begin{eqnarray*} x_m:=\chi_{[1-\alpha;\, 1)}\left(\{m\alpha +\theta\}\right)\quad \textrm{or}\quad x_m:= \chi_{(1-\alpha;\, 1]}\left(\{m\alpha +\theta\}\right). \end{eqnarray*} Here, $ \{x\}$ denotes the fractional part of $ x\in\Raa$, $ \chi_E$ the characteristic function of a set $ E\subset\Raa$ and $ \alpha$ and $ \theta$ are two real numbers such that $ \alpha\in\Raa\backslash\Qaa$ and $ \theta\not\in \alpha\Zaa+\Zaa$.

The following result is established in [Bellissard et al.1989] and [Damanik et al.2000].

Another measure of the complexity of a sequence has been introduced by [Kamae and Zamboni2002a, Kamae and Zamboni2002b]. It is defined as follows (with the natural modification if the sequence is single sided): for $ n\ge 1$, \begin{eqnarray*} p^*(n):=\sup_{0=\tau(0)< \cdots< \tau(n-1)}\#\left\{x_{m+\tau(0)}\cdots x_{m+\tau(n-1)}\, : \, m\in\Zaa\right\}, \end{eqnarray*} where $ \tau(0), \ldots, \tau(n-1)$ are integers. It is not difficult to see that if $ \boldsymbol{x}$ is an aperiodic sequence, then $ p^*(n)\ge 2n$ for all $ n\ge 1$. The sequence $ \boldsymbol{x}$ is pattern Sturmian if $ p^*(n)=2n$ for all $ n\ge 1$. Note that a Sturmian sequence is necessarily pattern Sturmian. The converse inclusion, however, does not hold.

With respect to the properties of the Schrödinger operator introduced in Theorem 2.1.1 above, one can expect the following:

The spectrum of Schrödinger operators associated with quasicrystal models in higher dimensions is not well understood. Consider for example the Penrose tiling and the corresponding graph $ (V, E)$, where $ V$ is the vertex set and $ E$ the set of edges. Define the operator $ H$ in the space $ l^2(V)$ as follows: for any $ \psi\in l^2(V)$ and any $ v\in V$, let \begin{eqnarray*} [H\psi](v):= \sum_{w\, : \,(v,w)\in E}\left(\psi(w)-\psi(v)\right). \end{eqnarray*}

Another example of a two dimensional problem arises when considering a two dimensional potential $ V$ that can be written as a sum of two one dimensional potentials $ s_1^{\lambda_1}$ and $ s_2^{\lambda_2}$. Here, $ \lambda_1, \lambda_2\in\CV$ and, for $ j\in\{1,2\}$ and $ k\in\Zaa$, \begin{eqnarray*} s_j^{\lambda_j}(k) := \lambda_j\cdot \chi_{[1-\gamma,1)}(\{k \gamma\}) \end{eqnarray*} with $ \gamma = \frac{\sqrt{5}-1}{2}$. Thus, for any $ m, n\in \Zaa$, \begin{eqnarray*} V(m,n) := s_1^{\lambda_1}(m)+s_2^{\lambda_2}(n). \end{eqnarray*} The corresponding Schrödinger operator $ H$ in the space $ l^2(\Zaa^2)$ is defined as follows: for $ \psi\in l^2(\Zaa)$ and $ (m,n)\in\Zaa^2$, \begin{eqnarray*} [H\psi](m,n)&:=& \psi(m+1, n)+\psi(m-1,n)+\psi(m,n+1)\\ &&+\,\psi(m,n-1)+V(m,n)\cdot\psi(m,n). \end{eqnarray*} The spectrum of this operator is expected to exhibit a very particular structure for some values of the parameters $ \lambda_1$ and $ \lambda_2$:

For more details on the concept of Cantorval, see [Mendes and Oliveira1994]. With obvious modifications, Conjecture 2.1.2 is expected to be true in higher dimensions as well.

One of the long-standing open problems in the field of mathematical quasicrystals is to determine which tiling dynamical systems (or Delone dynamical systems) have a pure point dynamical spectrum and thus a pure point diffraction pattern. For cut-and-project sets and tilings, this is the case by construction, but for inflation tilings the situation is not as clear. It is known ([Solomyak1997]) that a self-similar inflation tiling has a non-trivial pure point component in its spectrum if, and only if, the scaling factor of the inflation is a Pisot number $ \lambda$; that is, a real algebraic integer $ \lambda> 1$ all of whose conjugates are strictly smaller than one in modulus. This does not mean, however, that the spectrum is pure point. There is an algorithm ([Sirvent and Solomyak2002], [Solomyak1997]) that enables one to check whether a given tiling has pure point spectrum. Nevertheless, simple criteria that are easy to check or known to be true for whole classes of tilings are missing.

The Pisot Substitution Conjecture (see also the recent review [Akiyama et al.2015]) states the following:

Often, the additional assumption that $ M$ is unimodular is made so that $ \lambda$ is a unit in the ring $ \mathbb{Z}[\lambda]$. So far, this has not really helped to prove the conjecture.

Extensive computer search ([Akiyama et al.2014]) has failed to produce a counter-example but a general proof is also missing. There are some partial results. The conjecture is known to be true in the two tile case ($ \lambda$ a quadratic irrational) ([Hollander and Solomyak2003]). Also, it has been recently been proved for the class of inflation rules which are injective on the first tile and constant on the last tile ([Barge2016]) and also for $ \beta$-substitutions ([Barge2015b]) (which do not generally satisfy the conditions of the Pisot Substitution Conjecture).

One problem with the Pisot Substitution Conjecture is that the irreducibility of the characteristic polynomial of $ M$ is not invariant under topological conjugacies, whereas the spectral type of the dynamical system is. This has led to the statement of Pisot type conjectures with additional assumptions of a topological nature. The Homological Pisot Conjecture ([Barge et al.2012]) is in this vein:

This was later extended to the non-unimodular case in the form of the Coincidence Rank Conjecture ([Barge2015a]):

The coincidence rank is the multiplicity (almost everywhere) of the factor map to the maximal equicontinuous factor of the tiling dynamical system. It must be one for pure point spectrum.

We first briefly describe the construction of a Pinwheel Tiling following Conway and Radin—see [Conway and Radin1998] and [Radin1994] for further details and [Moustafa2010] for some of its properties.

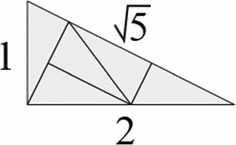
Let $ \mathcal{T}$ be a right triangle with side lengths 1, 2 and $ \sqrt{5}$. As noticed by Conway, $ \mathcal{T}$ can be divided into five isometric copies of its image by a dilation of factor $ 1/\sqrt{5}$—see Fig. 1. Figures 1 and 2 are taken from Wikipedia.   × ¹ A Pinwheel Tiling is then defined as a tiling of the plane whose tiles are isometric copies of $ \mathcal{T}$, in which a tile may intersect another tile only either on a whole side or on half the length 2 side, and such that the following property holds: the tiles of any Pinwheel Tiling can be grouped in sets of five into homothetic tiles, so that these homothetic tiles form (up to rescaling) a new Pinwheel Tiling.

There are uncountably many Pinwheel Tilings. See Fig. 2 below for an example.

Figure 1 Conway triangle decomposition into homothetic smaller triangles.

Figure 2 A Pinwheel tiling.

All Pinwheel Tilings are locally indistinguishable (i.e. any cluster which occurs in one Pinwheel Tiling, occurs in all such tilings) and share the property that tiles appear in infinitely many orientations. Choose a reference point (a natural choice is the point at coordinates $ (1/2,\, 1/2)$ with respect to the vertex point at the right-angled corner of the triangular tile) and consider a uniform Dirac comb obtained by placing a point measure at each reference point. The diffraction measure is the Fourier transform of the autocorrelation and is a well-defined positive measure. It is known that this measure has circular symmetry ([Moody et al.2006]) and, as a consequence, the only pure point part of it is the trivial point measure at the origin, which is related to the density (equal to one in this case). Apart from this point measure, the diffraction measure is continuous. However, note that a measure concentrated on 'sharp rings' (so that the measure is 'pure point in the radial direction') is a singular continuous measure in the plane as well.

There are arguments that support the existence of such 'sharp rings' in the diffraction measure of the pinwheel tiling ([Baake et al.2007]) similarly to what one would observe for a rotation-averaged square lattice arrangement of point masses. Numerical investigations also indicate the presence of additional components which might be absolutely continuous ([Baake et al.2007, Grimm and Deng2011]). However, none of these properties has yet been proved.

Let $ \alpha, \beta\in\Raa$ be such that $ 1, \alpha$ and $ \beta$ are $ \Qaa$-linearly independent. Let $ Y(\alpha, \beta)$ be a canonical cut-and-project set (this concept is defined in [Haynes et al.2016a]) formed using the subspace \begin{eqnarray*} E(\alpha, \beta):= \left\{(x,y, \alpha x + \beta y)\: : \, x,y\in\Raa \right\} \, \subset \, \Raa^3. \end{eqnarray*} Given a shape $ \Omega\subset E(\alpha, \beta)$, let $ \xi_{(\alpha, \beta)}(\Omega)$ denote the set of different frequencies of patches of shape $ \Omega$ in $ Y(\alpha, \beta)$ which occur in $ E(\alpha, \beta)$. Precise definitions of these terms are given in [Haynes et al.2016c] and here we are considering "type 2 patches".

Let $ M,N\in\Naa$ and \begin{eqnarray*} S_{(\alpha, \beta)}(M,N):= \left\{\{m\alpha+n\beta\}\, : \, 0\le m< M, \, 0\le n< N\right\}, \end{eqnarray*} where $ \{x\}$ denotes the fractional part of $ x\in\Raa$. Depending on the choice of the shape $ \Omega$, the cardinality of $ \xi_{(\alpha, \beta)}(\Omega)$ is closely related to the number $ G_{(\alpha, \beta)}(M,N)$ of distinct lengths of the component intervals of $ \mathbb{T}\backslash S_{(\alpha, \beta)}(M,N)$ for specific choices of $ M$ and $ N$ (here, $ \mathbb{T}=\Raa/\Zaa$ denotes the one-dimensional torus). For instance, the number of different frequencies for a two-to-one cut-and-project set when the window is an interval is at most 3. This is just another formulation of the Three Distance (or Steinhaus) Theorem and amounts to saying that $ G_{(\alpha, \beta)}(1, N)\le 3$ for any $ N\ge 1$.

The precise definition of an aligned square (resp. of an aligned rectangle) can be found in [Haynes et al.2016b].

It can be shown ([Haynes et al.2016c]) that (1) implies that $ \sup_{N\in\Naa}G_{(\alpha, \beta)}(N, N)=+\infty$. It was conjectured by Erdös ([Geelen and Simpson1993]) that the latter equation should hold whenever $ 1, \alpha$ and $ \beta$ are $ \Qaa$-linearly independent. This conjecture was disproved in [Bleher et al.2012], where it was established that the set of $ (\alpha, \beta)$ for which $ \sup_{N\in\Naa}G_{(\alpha, \beta)}(N, N)\, < \, +\infty$, although of zero Lebesgue measure, has full Hausdorff dimension. It is an open problem to determine whether there exists a pair $ (\alpha, \beta)$ such that $ \sup_{N\in\Naa}G_{(\alpha, \beta)}(N, N)\, = \, +\infty$.

The following is a seemingly easier version of the previous problem.

There is currently no known example of a pair $ (\alpha, \beta)$ for which (2) holds. Using the arguments in [Haynes et al.2016b, Haynes et al.2016c], it can be shown that any such pair satisfies the equation

Consider a tiling and the corresponding tiling space $ \Omega$ in dimension $ d\ge 1$. In the case of a word $ w$ over a finite alphabet (the tiling is then one-dimensional), the complexity function $ n\mapsto p(n)$ corresponding to $ w$ counts the number of subwords of $ w$ of length $ n$. In higher dimensions, the complexity function of a tiling counts in an analogous way the number of patches of radius $ n$ (up to translation)—see [Lagarias and Pleasants2003] for details.

In the case of a canonical (in particular, irrational and aperiodic) cut-and-project tiling, it is known ([Julien2010], Theorem 5.1) that the complexity function grows like $ O(n^d)$ if, and only if, the groups of cohomology over $ \Qaa$ of the tiling space are finitely generated. In other words, with usual notation, \begin{eqnarray*} p(n)=O(n^d)\, \iff\, \textrm{rk}(H^*(\Omega, \Qaa))< \infty. \end{eqnarray*}

The situation is not as well understood in the non-cut-and-project setup. For instance, there exist tilings in any dimension $ d\ge 1$ such that the corresponding tiling spaces have finitely generated groups of cohomology over the rationals whereas their complexity function grows faster than any polynomial—see, e.g., Proposition 6.20 in [Julien2010]. In dimension $ d=1$ however, the converse can be settled in the affirmative ([Julien2010], Proposition 6.7): if $ p(n)=O(n)$, then $ \textrm{rk}(H^1(\Omega, \Qaa))< \infty$. The following problem is concerned with a generalization of this result in higher dimensions:

Note that the result fails already in dimension one if one considers cohomologies over $ \Zaa$ rather than over $ \Qaa$. Indeed, the substitution defining the Thue–Morse sequence is primitive and therefore ([Queffélec2010]) the corresponding complexity function is bounded above by a linear function. Besides, one can show ([Anderson and Putnam1998]) that \begin{eqnarray*} H^1(\Omega_{TM}, \Zaa)\,\simeq\, \Zaa\left[\frac{1}{2}\right] \oplus \Zaa. \end{eqnarray*} In particular, $ H^1(\Omega_{TM}, \Zaa)$ is not finitely generated over $ \Zaa$.

In this direction, it has been shown ([Navas2016]) that the conclusion of Problem 2.6.1 is valid under the assumption of linear repetitivity (LR) or under the assumption of Burago–Kleiner (BK). Both of the these conditions imply that a Delone set is BL to a lattice. The reader is referred to [Burago and Kleiner1998] for an actual definition of the BK condition, which is technical. It is concerned with the speed of convergence of the number of points of a Delone set inside larger and larger balls.