The digit computation of $ \pi$ probably is one of the oldest research directions in mathematics. Due to Archimedes, we may consider the inscribed and circumscribed equilateral polygons for the unit circle. Let $ q_n$ (resp., $ Q_n$) be the perimeter of such an inscribed (resp., circumscribed) $ 3\cdot2^n$-gon. The sequences $ \{q_n\},\{Q_n\}$ obey the recurrence \begin{eqnarray*}Q_{n+1}=\frac{2q_nQ_n}{q_n+Q_n}, q_{n+1}=\sqrt{q_nQ_{n+1}}\end{eqnarray*} and both converge to $ 2\pi$. However this gives no closed formula.

A major breakthrough was made by Euler, Swiss-born (Basel) German–Russian mathematician. In his Saint-Petersburg Academy of Science talk (December 5, 1735) and, then, paper ([Euler1740]), he calculated ( literally ) that

Euler's idea was to use the identity \begin{eqnarray*} 1-\frac{z^2}{6}+\dots=\frac{\sin(z)}{z}=\prod_{n=1}^\infty \Big(1-\frac{z^2}{n^2 \pi^2}\Big), \end{eqnarray*} where the first equality is the Taylor series and the second equality is due to the fact that these two functions have the same set of zeroes. Equating the coefficients in $ z^2$, we get (1) . This reasoning was not justified until Weierstrass, but there appeared many other proofs. A nice exercise to get (1) is by considering the residues of $ \frac{\cot(\pi z)}{z^2}$.

We would like to mention here a rather elementary geometric proof of (1) which is contained in Cauchy's notes, ([Cauchy1821]).

Let $ \alpha=\frac{\pi}{2m+1}$. Then $ \sin (n\alpha)< n\alpha< \operatorname{tan} (n\alpha)$ for $ n=1,\dots,m$, see Fig. 1. Therefore, $ \cot^2(n\alpha)\leq \frac{1}{n^2\alpha^2}\leq \csc^2(n\alpha)$. Writing $ \frac{\sin ((2m+1)x)}{(\sin x)^{2m+1}}$ as a polynomial in $ \cot x$ and using the fact that $ \frac{\pi n}{2m+1}$ are the roots of this polynomial by Vieta's Theorem, we can find the sum of $ \cot^2\alpha$ and $ \csc^2\alpha$ for $ \alpha=\frac{\pi n}{2m+1}, n=1,\dots, m$.

Figure 1 An illustration for Cauchy's proof about the sum of reciprocals of the squares of natural numbers.

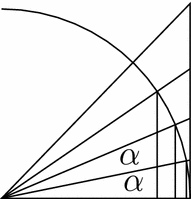
So, the above geometric consideration gives a two-sided estimate for $ \frac{1}{\pi^2}\sum_{n=1}^{m} \frac{1}{n^2}$ whose both sides converge to $ \frac{1}{6}$ as $ m\to\infty$.

Recall that $ SL(2,\ZZ)$ is the set of matrices $ \begin{pmatrix} a & b \\ c& d \end{pmatrix}$ with $ a,b,c,d\in\ZZ$ and $ ad-bc=1$. With respect to the matrix multiplication, $ SL(2,\ZZ)$ is a group. We may identify such a matrix with the pair $ (a,b),(c,d)\in\ZZ^2$ of lattice vectors. These vectors span the parallelogram of area one and, consequently, give a basis of $ \ZZ^2$.

Figure 2 The disc is inscribed into the square $ P_0$. Then, $ P_1$ is the only unimodular octagon circumscribing $ D^2$, which can be obtained by corner cuts of $ P_0$.

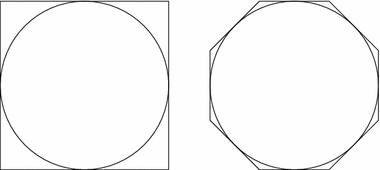
Let $ P_0=[-1,1]^2$, and $ D^2$ be the unit disk inscribed into $ P_0$, Fig. 2, left. Cutting all corners of $ P_0$ by tangent lines to $ D^2$ in the directions $ (\pm 1,\pm 1)$ results in the octagon $ P_1$, into which $ D^2$ is inscribed, Fig. 2, right.

Note that passing to $ P_{n+1}$ is unambiguous due to Remark 1.

Thus, we start with four vectors $ (1,0),(0,1),(-1,0),(0,-1)$—the outward directions for the sides of $ P_0$. To pass from $ P_n$ to $ P_{n+1}$, we order by angle all primitive vectors orthogonal to the sides of $ P_n$. Then, for each two neighboring vectors, we cut the corresponding corner of $ P_n$ by the tangent line to $ D^2$, orthogonal to their sum. In particular, every line with a rational slope tangent to $ D^2$ contains a side of $ P_n$ for $ n$ large enough.

We can reformulate the above observation as follows:

The area of the intersection of $ P_0{\setminus} D^2$ with the first quadrant is $ 1-\frac{\pi}{4}$. Therefore, Remark 2 and Lemma 2 prove (Ж) in the abstract.

The lattice perimeter of $ P_n$ is the sum of the lattice lengths of its sides. For example, the usual perimeter of the octagon $ P_1$ is $ 16(\sqrt 2-1)$, and the lattice perimeter is $ 4\sqrt 2$.

Proof.

One may ask what happens for other powers of $ f(a,b,c,d).$ There is a partial answer in degree 3, which also reveals the source of our formulae.

For every primitive vector $ w\in\ZZ^2$, a tangent line to $ D^2$ orthogonal to $ w$ is given by $ w\cdot p+|w|=0.$ Consider a piecewise linear function $ F:D^2\rightarrow \RR$ defined as

Performing verbatim the analysis of cropped tetrahedra applied to the graph of $ F$, one can prove the following lemma.

Now we describe the general idea behind (Ж), (ж). Denote by $ C\subset D^2$ the locus of all points $ p$ where the function $ F$ is not smooth. The set $ C$ is a locally finite tree (see Fig. 3). In fact, it is naturally a tropical curve (see [Kalinin and Shkolnikov2016], [Kalinin and Shkolnikov2017]). The numbers $ f(a,b,c,d)$ represent the values of $ F$ at the vertices of $ C$ and can be computed from the equations of tangent lines.

Figure 3 The plot of $ F$ and its corner locus (tropical analytic curve) $ C$ for a disc .

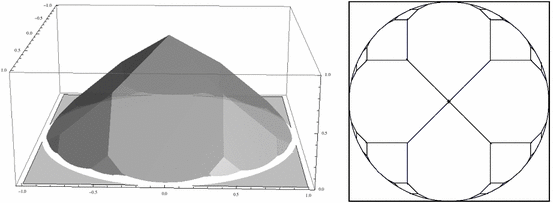
Below we list some directions, which we find interesting to explore. Coordinates on the space of compact convex domains For every compact convex domain $ \Omega$, we can define $ F_\Omega$ as the infimum of all support functions with integral slopes, exactly as in (2) . Consider the values of $ F_{\Omega}$ at the vertices of $ C_\Omega$, the corner locus of $ F_\Omega$. These values are the complete coordinates on the set of convex domains; therefore, the characteristics of $ \Omega$ (for example, the area) can be potentially expressed in terms of these values. How to relate these coordinates of $ \Omega$ with those of the dual domain $ \Omega^*$? Higher dimensions We failed to reproduce this line of arguments "by cropping" for three-dimensional bodies, but it seems that we need to sum up by all quadruples of vectors $ v_1,v_2,v_3,v_4$ such that $ \mathrm{ConvHull}(0,v_1,v_2,v_3,v_4)$ contains no lattice points. Zeta function We may consider the sum $ Z(s) = \sum f(a,b,c,d)^s$ as an analog of the Riemann zeta function. We can prove that $ Z(s)$ converges as long as $ s> 1/2$. Can we extend this function for complex values of $ s$? Other proofs It would be nice to give another proof of (Ж), (ж) with the methods which were used to prove (1) . Note that the vectors $ (a,b),(c,d)$ can be uniquely reconstructed from the vector $ (a+c,b+d)$, and our construction resembles the Farey sequence a lot. So we can think of $ f(a,b,c,d)$ as a kind of a measure on $ \QQ\cap [0,1]$, and can integrate a function along it. Can we interpret $ f(a,b,c,d)$ as a residue of a certain function at $ (a+b)+(c+d)i$? The Riemann zeta function is related to integers; could it be that $ f$ is related to the Gauss integers? Modular forms We can extend $ f$ to the whole $ SL(2,\ZZ)$. If both vectors $ (a,b),(c,d)$ belong to the same quadrant, we use the same definition. For $ (a,b),(c,d)$ from different quadrants, we could define \begin{eqnarray*} f(a,b,c,d)=\sqrt{a^2+b^2}+\sqrt{c^2+d^2}-\sqrt{(a-c)^2+(b-d)^2}. \end{eqnarray*} Then \begin{eqnarray*} \sum\limits_{m\in SL(2,\ZZ)}f(m) = \sum\limits_{\substack {a,b,c,d\in \ZZ \\ ad-bc=1}}f(a,b,c,d) \end{eqnarray*} is well defined. Can we naturally extend this function to the $ {\mathbb{C}}/SL(2,\ZZ)$? Can we make similar series for other lattices or tessellations of the plane?