On fields of meromorphic functions on neighborhoods of rational curves

It is well known (see Proposition  5.1 below for references) that the field of meromorphic functions on a \(2\)-dimensional neighborhood of the Riemann sphere with positive self-intersection is a finitely generated extension of , of transcendence degree at most \(2\). In recent papers  [5] , [6] , [8] examples of such neighborhoods were constructed for which this transcendence degree assumes all values from \(0\) through \(2\) (in particular, examples of non-algebraizable neighborhoods with transcendence degree \(2\) were found).

Now it seems natural to ask what fields may occur as such fields of meromorphic functions (in the case of transcendence degree \(1\) or \(2\), of course). It turns out that the answer to this question is simple and somehow disappointing. To wit, the main results of the paper are as follows.

Proposition 1.1.

Suppose that \(F\) is a non-singular connected complex surface and that there exists a curve \(C\subset F\), \(C\cong \PP ^1\), such that \((C\cdot C)>0\). Let be the field of meromorphic functions on \(F\).

If the transcendence degree of over is at least \(2\), then \(\M \cong \C (T_1,T_2)\) (the field of rational functions).

Proposition 1.2.

Suppose that \(F\) is a non-singular connected complex surface and that there exists a curve \(C\subset F\), \(C\cong \PP ^1\), such that \((C\cdot C)>0\). Let be the field of meromorphic functions on \(F\).

If the transcendence degree of over is \(1\), then \(\M \cong \C (T)\) (the field of rational functions).

Summing up, if \(F\) is a smooth and connected complex surface contaning a copy of the Riemann sphere with positive self-intersetion, then the field of meromorphic functions on \(F\) is isomorphic to either or \(\C (T)\) or \(\C (T_1,T_2)\).

Thus, the field of meromorphic functions without any additional structure cannot serve as an invariant that would help to classify neighborhoods of rational curves with positive self-intersection.

Proposition  1.2 agrees with the example from  [6], Section 3.2 .

The proof of Propositions  1.1 and  1.2 are based on the study of (embedded) deformations of the curve \(C\subset F\). Properties of such deformations are well known in the algebraic context; the classical paper  [7] implies a complete description of deformations of rational curves on arbitrary smooth complex surfaces, but this paper does not contain a description of deformations of rational curves passing through given points; I prove the necessary facts (Propositions  3.1 and  3.2 ) in the ad hoc manner, using a result of Savelyev  [11] .

The paper is organized as follows. In Section  2 we recall, following Douady  [4] , general facts on deformations of compact analytic subspaces in a given analytic space. In Section  3 we prove some pretty natural results on deformations of smooth rational curves in smooth (and not necessarily compact) complex surfaces; the results of this section do not claim much novelty. In Section  4 we establish some more specific properties of deformations of rational curves on surfaces. Finally, in Section  5 (resp.  6 ) we prove Proposition  1.1 (resp.  1.2 ).

In this section we recall (briefly and without proofs) the general theory (see  [4] for details). Suppose that \(F\) is an analytic space (in the applications we have in mind \(F\) will be a smooth complex surface). Then there exists the Douady space  \(\Do (F)\), which parametrizes all the compact analytic subspaces of \(F\). This means the following.

For any analytic space \(B\), a family of compact analytic subspaces of \(F\) with the base \(B\) is a closed analytic subspace \(\Ho \subset B\times F\) that is proper and flat over \(B\). Now the Douady space \(\Do (F)\) comes equipped with the universal family \(\Ho (F)\subset \Do (F)\times F\) of subspaces of \(F\) over \(\Do (F)\), which satisfies the following property: for any family over an analytic space \(B\) there exists a unique morphism \(B\to \Do (F)\) such that the family over \(B\) is induced, via this morphism, from the universal family over \(\Do (F)\). Applying this definition to the case in which \(B\) is a point (hence, a family over \(B\) is just an individual compact analytic subspace of \(F\)), one sees that there is a 1–1 correspondence between compact analytic subspaces of \(F\) and fibers of the projection \(\Ho (F)\to \Do (F)\).

At this point one has to say that the Douady space is not an analytic space: it is a more general object, which Douady calls a Banach analytic space. However, every point \(a\in \Do (F)\) has a neighborhood \(\Delta \ni a\) that is isomorphic to an analytic space in the usual sense.

This construction can be generalized as follows. If is a coherent analytic sheaf on \(F\), then there exists a Banach analytic space \(\Dou (\E )\) parametrizing coherent subsheaves \(\Sc \subset \E \) such that the quotient \(\E /\Sc \) has compact support. To be more precise, a family of subsheaves of with base \(B\) is a coherent subsheaf \(\varSigma \subset \pr _2^*\E \) on \(B\times F\) such that \(\pr _2^*\E /\varSigma \) is flat over \(B\) and \(\supp (\pr _2^*\E /\varSigma )\) is proper over \(B\), and there is a universal family of subsheaves of over \(\Dou (\E )\).

The space \(\Dou (\E )\) is also locally isomorphic to an analytic space. If one puts \(\E =\Oo _F\) in this construction, one obtains a canonical isomorphism \(\Do (F)\cong \Dou (\Oo _F)\).

If \(a\in \Dou (\E )\) is a point corresponding to the subsheaf \(\Sc \subset \E \), then one can define the Zariski tangent space \(T_a\Dou (\E )\) to \(\Dou (\E )\) at \(a\) as \(T_a\Delta \), where \(\Delta \subset \Dou (\E )\) is any neighborhood of \(a\) that is isomorphic to an analytic space. This Zariski tangent space is canonically isomorphic to \(\Hom (\Sc ,\E /\Sc )\) (see [4], Section 9.1, Remarque 3 ).

If a coherent sheaf is a subsheaf of a coherent sheaf and if \(\F /\E \) has compact support, then \(\Dou (\E )\) is naturally embedded in \(\Dou (\F )\) (a subsheaf of can be regarded as a subsheaf of ). This embedding induces injective homomorphisms of Zariski tangent spaces. Indeed, let \(\Spec \C [\eps ]/(\eps ^2)\) be the analytic space consisting of one point such that the ring of functions is \(\C [\eps ]/(\eps ^2)\). Then \(T_a\Dou (\E )\), as a set, is canonically bijective to the set of families of subsheaves of over the base \(\Spec \C [\eps ]/(\eps ^2)\) (ibid.). If \(\supp (\F /\E )\) is compact, any family of subsheaves of (over an arbitrary base) is automatically a family of subsheaves of , and different families of subsheaves of , being different subsheaves of \(\pr _2^*\E \), are ipso facto different subsheaves of \(\pr _2^*\F \).

In the sequel we will be using the following notation.

In this section we state and prove two auxiliary results concerning deformations of smooth rational curves on complex surfaces. These results are well known for deformations of curves on which no restrictions are imposed. For example, Proposition  3.1 below follows immediately from the main result of  [7] , and its algebraic-geometric counterpart (for smooth algebraic surfaces over a field of characteristic zero) follows immediately from the theorem in Lecture 23 of  [9] . However, I did not manage to find a suitable reference for deformations of curves passing through given points.

We will be using the general theory from Section  2 in the following setting. \(F\) will always be a smooth and connected complex surface, \(C\subset F\) will be a complex submanifold isomorphic to \(\PP ^1\) (the Riemann sphere), and we will always assume that the self-intersection index \(d=(C\cdot C)\) is non-negative. By \(\Do (F,C)\) we will mean an unspecified open subset of \(\Do (F)\) that contains the point corresponding to \(C\subset F\) and is isomorphic to an analytic space. The reader will check that this indeterminacy of definition does not affect the arguments that follow.

Moreover, suppose that \(S=\{\lst pm\}\subset C\) is a subset of cardinality \(m\le d=(C\cdot C)\). Let \(\Ii _S\subset \Oo _F\) be the ideal sheaf of the analytic subset \(S\subset F\). If \(\Ii \subset \Ii _S\) is a coherent subsheaf, then it follows from the exact sequence

\begin{equation*} 0\to \Ii _S/I\to \Oo _F/\Ii \to \Oo _F/\Ii _S\to 0 \end{equation*}

that \(\supp (\Oo _F/\Ii )= \supp (\Ii _S/I)\cup S\), so \(\supp (\Ii _S/I)\) is compact if and only if \(\supp (\Oo _F/\Ii )\) is compact. Hence, the Douady space \(\Dou (\Ii _S)\) parametrizes the (ideal sheaves of) compact analytic subspaces of \(F\) containing the subset \(S\). An unspecified open subset of \(\Dou (\Ii _S)\) containing the point corresponding to \(C\) (strictly speaking, to the ideal sheaf of \(C\), which is a subsheaf of \(\Ii _S\)) and isomorphic to an analytic space, will be denoted by \(\Do (F,C,S)\). In view of the natural embedding of \(\Dou (\Ii _S)\) into \(\Dou (\Oo _F)=\Do (F)\) we will always assume that \(\Do (F,C,S)\subset \Do (F,C)\).

Extending Notation  2.1 , we will denote by \(C_a\subset F\) the analytic subspace of \(F\) corresponding to the point \(a\in \Do (F,C,S)\).

Let \(a\in \Do (F,C)\) be the point corresponding to \(C\subset F\), and let \(\Ii _C\cong \Oo _F(-C)\) be the ideal sheaf of \(C\subset F\). According to the general theory, the Zariski tangent space to \(\Do (F,C)\) at \(a\) is

\begin{multline*} T_b\Do (F,C,S)\cong \Hom _{\Oo _F}(\Ii _C,\Ii _S/\Ii _C)\\{}\cong \Hom _{\Oo _C}(\Ii _C/\Ii _C^2,\Ii _S)\cong \Nc _{F|C}\otimes \Oo _C(-S)\cong \Oo _C(d-m). \end{multline*}

The main results about deformations of \(C\subset F\) that we need are as follows.

A similar result, of which Proposition  3.1 is a particular case, holds for \(\Do (F,C,S)\).

We begin with a particular case, which is essentially contained in  [11] (and which follows from the main result of  [7] ).

Proof.

Let \(a\in \Do (F,C)\) be the point corresponding to \(C\subset F\). Since \(d=0\), one has \(\Nc _{F|C}\cong \Oo _C\), so it follows from ( 1 ) that \(\dim T_a\Do (F,C)=1\). But, according to the main result of  [11] , there exist a neighborhood \(W\supset C\) and an isomorphism \(\ph \colon W\to D\times C\), where \(D\) is the unit disk in , such that \(\ph (p)=(0,p)\) for any \(p\in C\). If one puts

\(\seteqnumber{0}{}{1}\)

\begin{equation*} \Gf =\{(z,x)\in D\times F\colon x\in W,\ \pr _1(\ph (x))=z\}, \end{equation*}

then the family induces a morphism \(\Phi \colon D\to \Do (F,C)\) such that \(\Phi (0)=a\) (the point corresponding to \(C\)) and \(\Phi \) is 1–1 onto its image. Hence, \(\dim _a\Do (F,C)\ge 1\). Since \(\dim T_a\Do (F,C)=1\), one concludes that \(\Do (F,C)\) is a smooth \(1\)-dimensional complex manifold in a neighborhood of \(a\).

To prove Proposition  3.2 in full generality, we will need two simple lemmas.

Lemma 3.4.

If \(p\colon \Ho \to D\), where \(D\) is the unit disk in , is a proper and flat morphism of analytic spaces, and if the fiber \(p^{-1}(0)\) is reduced and isomorphic to \(\PP ^1\), then there exists an \(\eps \in (0;1)\) such that the fiber \(f^{-1}(a)\) is also reduced and isomorphic to \(\PP ^1\) whenever \(|a|<\eps \).

Sketch of proof.

It is easy to see that there exists an \(\eps >0\) such that \(p^{-1}(D_\eps )\to D_\eps \) is a proper submersion of complex manifolds. Hence, topologically it is a locally trivial bundle, so all the fibers are homeomorphic to \(S^2\), whence the result.

Proof.

Proof of Proposition  3.2 .

Choose \(d-m\) distinct points \(\lst q{d-m}\in C\setminus S\). Let \(\bar F\) be the blowup of \(F\) at the points \(\lst pm,\lst q{d-m}\), let \(\sigma \colon \bar F\to F\) be the corresponding blowdown morphism, and let \(\bar C\subset \bar F\) be the strict transform of \(C\). One has \(\bar C\cong \PP ^1\) and \((\bar C,\bar C)=0\). Let \(\bar a\in \Do (\bar F,\bar C)\) be the point corresponding to \(\bar C\), and let \(a\in \Do (F,C,S)\) be the point corresponding to \(C\).

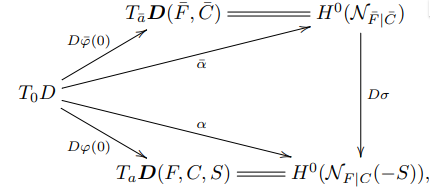
Applying Lemma  3.3 to the pair \((\bar F,\bar C)\), one concludes that there exists a family \(\bar \Ho _0\subset D\times \bar F\), where \(D\) is the unit disk in the complex plane, such that its fiber over \(0\) is \(\bar C\subset \bar F\) and, for the induced mapping \(\bar \ph \colon D\to \Do (\bar F,\bar C)\), its derivative \(D\bar \ph (0)\colon T_0D\to T_{\bar a}\Do (\bar F,\bar C)\) is non-degenerate.

If we put \(\Ho _0=(\mathrm {id}\times \sigma )(\bar \Ho _0)\subset D\times F\), then \(\Ho _0\) is a family of analytic subspaces in \(F\) containing \(S\); its fiber over \(0\) is \(C\). Let \(\ph \colon D\to \Do (F,C,S)\) be the mapping induced by this family.

It is clear that the diagram

where the vertical arrow is induced by the natural homomorphism \(\Nc _{\bar F|\bar C}\to \sigma ^*\Nc _{F|C}\), is commutative. It follows from (the proof of) Lemma  3.3 that \(\bar \alpha (\partial /\partial z)\), where \(z\) is the coordinate on \(D\), is a nowhere vanishing section of \(\Nc _{\bar F|\bar C}\cong \Oo _{\bar C}\); since the derivative of the mapping \(\sigma \) is non-degenerate outside \(\sigma ^{-1}\{\lst pm,\lst q{d-m}\}\), the section \(\alpha (\partial /\partial z)=D\sigma (\bar \alpha (\partial /\partial z))\) is not identically zero. Hence, \(\ph \) induces an embedding of a possibly smaller disk \(D_\eps \subset D\) in \(\Do (F,C,S)\).

Moreover, since \(\sigma \) maps each of the curves \(\sigma ^{-1}(p_i)\), \(\sigma ^{-1}(q_j)\) to a point, and since each of these curves is transverse to \(\bar C\), the section \(\alpha (\partial /\partial z)\) vanishes at \(\lst pm,\lst q{d-m}\), so \(\alpha (\partial /\partial z)\) spans the \(1\)-dimensional linear space

\(\seteqnumber{0}{}{1}\)

\begin{equation} \label {eq:1-dim} H^0(\Nc _{F|C}(-S)(-q_1-\dots -q_{d-m}))\subset H^0(\Nc _{F|C}(-S)) =T_a\Do (F,C,S). \end{equation}

In the argument that follows we will assume that \(d-m\ge 2\), so that the words about Veronese curves in \(\PP ^d\) and \(\PP ^{d-m}\) make sense; we leave it to the reader to modify the wording for the case \(d-m=1\).

Keeping the above in mind, identify \(C\) with \(\PP ^1\) and \(\Nc _{F|C}\) with \(\Oo _{\PP ^1}(d)=\Oo _C(d)\), embed \(C\) in \(\PP ^d\) with the complete linear system \(|\Oo _C(d)|\) to obtain a Veronese curve \(C_d\subset \PP ^d\), and project \(C_d\) from \(\PP ^d\) to \(\PP ^{d-m}\), the center of projection being the linear span of the images of the points . The image of this projection will be a Veronese curve \(C_{d-m}\subset \PP ^{d-m}\); denote the resulting isomorphism between \(C\) and \(C_{d-m}\) by \(\ph \colon C\to C_{d-m}\).

One has

\(\seteqnumber{0}{}{2}\)

\begin{equation*} \PP ^{d-m}=\PP ((H^0(\Nc _{F|C}(-S))^*); \end{equation*}

for any \(d-m\) distinct points \(\lst q{d-m}\in C\setminus S\) the points \(\ph (q_1),\dots ,\ph (q_{d-m})\) span a hyperplane in \(\PP ^{d-m}\), and the linear span \(\langle \ph (q_1),\dots ,\ph (q_{d-m})\rangle \) is the projectivization of

\(\seteqnumber{0}{}{2}\)

\begin{equation*} \Ann (H^0(\Nc _{F|C}(-S)(-q_1-\dots -q_{d-m}))) \subset H^0(\Nc _{F|C}(-S))^*. \end{equation*}

Now the hyperplanes in \(\PP ^{d-m}\) that are transverse to \(C_{d-m}\) form a non-empty Zariski open subset in \((\PP ^{d-m})^*=\PP (H^0(\Nc _{F|C}(-S)))\) and any such hyperplane intersects \(C_{d-m}\) at \(d-m\) distinct points that are of the form \(\ph (q_1),\dots , \ph (q_{d-m})\), where \(\lst q{d-m}\in C\setminus S\). Thus, the linear subspaces of the form ( 2 ) fill a non-empty Zariski open subset in \(\PP (T_a\Do (F,C,S))\) as we vary \(\lst q{d-m}\in C\setminus S\), so the hypotheses of Lemma  3.5 are satisfied if one puts \(Y=\ph (D)\), hence the smoothness is established. Now the assertion to the effect that the fibers are isomorphic to \(\PP ^1\) follows from Lemma  3.4 .

Suppose that \(F\) is a smooth and connected complex surface and \(C\subset F\) is a curve that is isomorphic to \(\PP ^1\) and \((C\cdot C)\ge 0\). In the definition below we use Notation  2.1 .

Proof.

Proof.

In this section we prove Proposition  1.1 . We begin with two simple observations.

Proposition 5.1.

If \(F\) is a smooth connected complex surface that contains a curve \(C\subset \PP ^1\) such that \((C\cdot C)>0\), then the field of meromorphic functions \(\M (F)\) is finitely generated over and \(\trdeg _\C \M (F)\le 2\).

Proof.

Theorem 2.1 from  [10] asserts that there exists a pseudoconcave neighborhood \(U\supset C\). According to [1], Théorème 5 , the field \(\M (U)\) is finitely generated over and \(\trdeg _\C \M (U)\le 2\). Observe that \(\M (F)\) embeds in \(\M (U)\) as an extension of ; since any sub-extension of a finitely generated extension of fields is also finitely generated and the transcendence degree is additive in towers, we are done.

Proof.

Since \(\M (F)\) embeds into \(\M (U)\), it follows immediately from the two-dimensional Lüroth theorem.

Now we may begin the proof of Proposition  1.1 . Thus, let \(F\) be a smooth connected complex surface such that \(\trdeg _\C \M (F)\ge 2\) and let \(C\cong \PP ^1\) be a curve (one-dimensional complex submanifold) such that \((C\cdot C)=d>0\). Let \(W\subset F\) be a good neighborhood of \(C\) in the sense of Definition  4.1 . We are to prove that \(\M (F)\cong \C (T_1,T_2)\); by virtue of Lemma  5.2 it suffices to prove that \(\M (W)\cong \C (T_1,T_2)\).

Since \(\trdeg _\C \M (F)\le 2\) by virtue of Proposition  5.1 and \(\trdeg _\C \M (F)\ge 2\) by hypothesis, one has \(\trdeg _\C \M (F)=2\). Now \(\M (F)\) is isomorphic to a subfield of \(\M (W)\), so \(\trdeg _\C \M (W)\ge 2\). Since Proposition  5.1 implies that \(\trdeg _\C \M (W)\le 2\) and \(\M (F)\) is finitely generated over , one concludes that \(\M (W)\) is a finitely generated extension of , of transcendence degree \(2\). Hence, \(\M (W)=\C (f,g,h)\), where the meromorphic functions \(f\) and \(g\) are algebraically independent over and \(h\) is algebraic over \(\C (f,g)\) (of course, if one may set \(h=0\), there is nothing to prove). Denote by \(P\) an irreducible polynomial in three independent variables \(F\), \(G\), and \(H\) such that \(P(f,g,h)\) is identically zero.

Now let \(Y\subset \C ^3\) be the affine algebraic surface that is the zero locus of \(P\), and let \(X\subset \PP ^N\) be a smooth projective model of \(Y\).

Denote by \(V\subset W\) the open subset on which each of the meromorphic functions \(f\), \(g\), and \(h\) is well defined and consider the holomorphic mapping \(\Phi \colon V\to Y\) defined by the formula \(x\mapsto (f(x),g(x),h(x))\). The mapping \(\Phi \) extends to a meromorphic mapping from \(W\) to \(\bar Y\subset \PP ^3\), where \(\bar Y\) is the closure of \(Y\); composing this meromorphic mapping with a birational mapping \(\bar Y\dashrightarrow X\), one obtains a meromorphic mapping \(\Phi _1\colon W\dashrightarrow X\).

Assuming this lemma for a while, let us finish the proof of Proposition  1.1 .

Our construction of the surfaces \(X\) and \(Y\) implies that \(\M (X)\cong \M (W)\); hence, to prove Proposition  1.1 it suffices to show that \(\M (X)\cong \C (T_1,T_2)\). We will derive this fact from the Castelnuovo rationality criterion (see for example [3], Chapter VI, 3.4 ), which may be stated as follows.

  

Theorem 5.4 (Castelnuovo) .

Suppose that \(X\) is a smooth projective surface over . Then \(\M (X)\cong \C (T_1,T_2)\) if and only if \(H^0(X,\Omega ^1_X)=0\) and \(H^0(X,\omega _X^{\otimes 2})=0\).

Here, \(H^0(X,\Omega ^1_X)\) is the space of holomorphic 1-forms on \(X\) and \(H^0(X,\omega _X^{\otimes 2})\) is the space of holomorphic 2-forms of weight \(2\) on \(X\); we are to check that, for our surface \(X\), both these linear spaces do not contain non-zero elements.

To begin with, observe that if \(\eta \) is a holomorphic covariant tensor field on \(X\) that is not identically zero, then \(\Phi _1^*\eta \) is a holomorphic tensor field on \(W\setminus I\), where \(I\) is the indeterminacy locus of \(\Phi _1\), and, in view of Lemma  5.3 , \(\Phi _1^*\eta \) is not identically zero. Since \(I\) is a discrete subset of the complex surface \(W\), \(\Phi _1^*\eta \) extends to a tensor field on the entire \(W\). Thus, to show that \(H^0(X,\Omega ^1_X)=0\) and \(H^0(X,\omega _X^{\otimes 2})=0\) it suffices to show that \(H^0(W,\Omega ^1_W)=0\) and \(H^0(W,\omega _W^{\otimes 2})=0\), that is, that there are no non-trivial holomorphic \(1\)-forms or \(2\)-forms of weight \(2\) on \(W\). We deal with these two types of tensor fields separately.

The absence of holomorphic \(1\)-forms. This is just the following lemma, which will be used in Section  6 as well.

Lemma 5.5.

Suppose that \(F\) is a non-singular complex surface, \(C\subset F\) is a curve such that \(C\cong \PP ^1\) and \((C\cdot C)>0\), and \(W\) is a good neighborhood of \(C\). Then any holomorphic \(1\)-form on \(W\) is identically zero.

Proof.

Suppose that \(\omega \) is such a form. Proposition  4.3 implies that, for any \(x\in W\) there exist curves \(C_1,C_2\subset W\), \(C_1\cong C_2\cong \PP ^1\) such that \(C_1\cap C_2\ni x\) and \(C_1\) and \(C_2\) are transverse at \(X\). Since there are no non-zero holomorphic \(1\)-forms on the Riemann sphere, the restriction of \(\omega \) to both \(C_1\) and \(C_2\) is identically zero. Hence, the linear functional \(\omega _x\) that \(\omega \) induces on \(T_xW\) is zero on \(T_xC_1,T_xC_2\subset T_xW\). Since \(C_1\) and \(C_2\) are transverse at \(x\), these two linear spaces span the entire \(T_xW\), so \(\omega _x=0\). Since \(x\in W\) was arbitrary, \(\omega =0\) and we are done.

The absence of holomorphic \(2\)-forms of weight \(2\). Recall that differential \(2\)-forms of weight \(2\) on a surface \(G\) have, in local coordinates \((z,w)\), the form \(f(z,w)(dz\wedge dw)^2\). If \(\omega \) is such a form, then, for any point \(x\in G\), \(\omega _x\) is a mapping from \(T_xG\times T_xG\) to ; this mapping is uniquely determined by its value at a given pair of linearly independent tangent vectors.

Lemma 5.6.

If \(G=U\times \PP ^1\), where \(U\) is an open subset of , then there is no non-trivial holomorphic \(2\)-form of weight \(2\) on \(G\).

Proof.

Suppose that \(\omega \) is such a form. If \(z\) is the coordinate on \(U\subset \C \), then there exists a nowhere vanishing holomorphic vector field \(\partial /\partial z\) on \(G\). For any \(b\in U\), put \(C_b=\{b\}\times \PP ^1\). To show that \(\omega =0\) it suffices to show that for any \(b\in U\) and \(x\in C_b\) one has \(\omega _x(\partial /\partial z,v)=0\), where \(v\in T_xC_b\) is a nonzero tangent vector.

Consider the tensor field \(\eta =i_{\partial /\partial z}\omega \) (the contraction of \(\omega \) with \(\partial /\partial z\)), which is a family of functions \(\eta _x\colon T_xG\to \C \) for all \(x\in G\), \(\eta _x(w)=\omega _x(\partial /\partial z,w)\) for \(w\in T_xG\). The field \(\omega \) is a holomorphic section of \(\Sym ^2\Omega ^1_G\), and its restriction to each \(C_b\) is a section of \(\omega _{C_b}^{\otimes 2}\), i.e., a quadratic differential on \(C_b\), i.e., a section of \(\Oo _{C_b}(-4)\); such a holomorphic section must be identically zero, so, for any \(x\in C_b\) and any \(v\in T_xC_b\), \(\omega _x(\partial /\partial z,v)=\eta (v)=0\), and we are done.

Now suppose that \(\omega \) is a differential \(2\)-form of weight \(2\) on \(W\). To show that \(\omega =0\), pick \(d\) distinct points \(\lst pd\in C\), where \(d=(C\cdot C)\), and let \(\bar W\) be the blowup of \(W\) at and \(\bar C\subset \bar W\) be the strict transform of \(C\). It suffices to show that \(\sigma ^*\omega =0\), where \(\sigma \colon \bar W\to W\) is the blowdown morphism, and it will suffice to show that \(\sigma ^*\omega =0\) on a non-empty open subset of \(\bar W\). Since \(\bar C\cong \PP ^1\) and \((\bar C\cdot \bar C)=0\), it follows from the main result of Savelyev's paper  [11] that a neighborhood of \(\bar C\) in \(\bar W\) is isomorphic to \(U\times \PP ^1\), where \(U\) is an open subset of \(\C \). Now Lemma  5.6 applies.

This completes the proof of Proposition  1.1 modulo Lemma  5.3 .

Proof of Lemma  5.3 .

It suffices to prove this assertion for \(\Phi \colon V\to Y\subset \C ^3\) instead of \(\Phi _1\). Moreover, if \(\pi \colon Y\to \C ^2\) is the projection defined by forgetting the third coordinate, then the derivative of \(\pi \) is non-degenerate on a non-empty Zariski open subset of the smooth locus of \(Y\); hence, it suffices to establish the existence of such a set \(O\) for the mapping \(\Psi =\pi \circ \Phi \colon V\to \C ^2\), \(\Psi \colon x\mapsto (f(x),g(x))\).

The mapping \(\Psi \) extends to a meromorphic mapping \(W\dashrightarrow \PP ^2\) defined, in the homogeneous coordinates, by \(x\mapsto (1:f(x):g(x))\); abusing the notation, we will denote this meromorphic mapping by \(\Psi \) as well. The indeterminacy locus of the meromorphic mapping \(\Psi \) is a discrete subset of \(W\).

If there exists at least one point \(x\in W\) where \(\Psi \) is defined and \(D\Psi (x)\) is non-degenerate, we are done. Assume now that the derivative of \(\Psi \) is degenerate at any point where \(\Psi \) is determined; we will show that this assumption leads to a contradiction.

Let \(\Delta \subset \Do (F,C)\) be the open subset such that \(W=q(p^{-1}(\Delta ))\), where \(p\colon \Ho \to \Do (F)\) and \(q\colon \Ho \to F\) are the canonical projections of the restriction of the universal family ; recall that the curve \(q(p^{-1}(b))\subset F\), where \(b\in \Delta \), is denoted by \(C_b\).

Observe that the restriction of \(\Psi \) to any \(C_b\) is a meromorphic, hence holomorphic, mapping from \(C_b\) to \(\PP ^2\). For any \(b_1,b_2\in \Delta \), \((C_{b_1}\cdot C_{b_2})=(C\cdot C)>0\), hence \(C_{b_1}\cap C_{b_2}\ne \varnothing \). Thus, if the restriction of \(\Psi \) to each \(C_b\) is constant, then \(\Psi \) is constant, which is nonsense. Hence, we may and will pick a \(b\in \Delta \) such that the restriction of \(\Psi \) to \(C_b\) is not constant. Put \(\Psi (C_b)=Z\subset \PP ^2\); it follows from the Chow theorem that \(Z\) is a projective algebraic curve.

Observe as well that the set of points \(x\in W\) where \(\Psi \) is defined and \(D\Psi (x)=0\) must have empty interior (otherwise \(\Psi \) would be constant). Hence, there exists a closed analytic subset \(D\) with empty interior such that, for any \(x\in W\setminus D\), \(\Psi \) is defined at \(x\) and \(\rank D\Psi (x)=1\). Hence, all the fibers of the restriction \(\Psi |_{W\setminus D}\) are smooth analytic curves in \(W\setminus D\).

Figure 1.

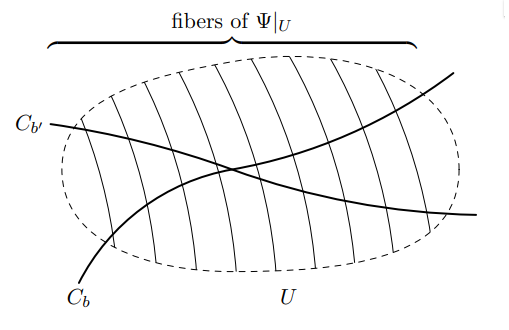
Pick a point \(x\in C_b\setminus D\) such that \(T_xC_b\) is not contained in \(\Ker D\Psi (x)\). There exists an open set \(U\ni x\), \(U\subset W\setminus D\) such that for any \(y\in C_b\cap U\) the set \(\Psi ^{-1}(\Psi (y))\) is a smooth analytic curve transverse to \(C\) at \(y\). Now for any \(b'\in \Delta \) that is close enough to \(b\) there exists a non-empty open set \(V\subset C_{b'}\cap U\) such that for any \(x'\in V\) there exists a point \(y'\in C_b\cap U\) such that \(\Psi ^{-1}(\Psi (y'))\cap C_{b'}\) contains \(x'\) (see Fig.  1 ).

Hence, \(\Psi (V)\subset \Psi (C_b)\); since \(V\) is a non-empty open subset of \(C_{b'}\), one concludes that \(\Psi (C_{b'})=\Psi (C_b)=Z\subset \PP ^2\). Since the curves \(C_{b'}\), for all \(b'\) close enough to \(b\), sweep, by virtue of Proposition  4.2 , an open subset of \(W\), one concludes that \(\Psi (W)\subset Z\). Since \(Z\) is an algebraic curve in \(\PP ^2\) and \(\Psi \) is defined by the formula \(x\mapsto (1:f(x):g(x))\), it follows that the meromorphic functions \(f\) and \(g\) are algebraically dependent, which yields the desired contradiction.

In this section we prove Proposition  1.2 . Its proof is similar to that of Proposition  1.1 , but simpler.

To wit, by virtue of Proposition  5.1 the field \(\M (F)\) is finitely generated over . Since \(\trdeg _\C \M (F)=1\), one has \(\M (F)=\C (f,g)\), where the meromorphic functions \(f\) and \(g\) are algebraically dependent over (if \(\M (F)\) is generated by one function, there is nothing to prove). Denote by \(P\) an irreducible polynomial in two independent variables \(F\) and \(G\) such that \(P(f,g)=0\); let \(Y\subset \C ^2\) be the affine curve that is the zero locus of \(P\), and let \(X\) be the smooth projective curve (aka compact Riemann surface) for which \(\M (X)\cong \M (Y)\).

Denote by \(V\subset F\) the open subset on which both \(f\) and \(g\) are well defined and consider the holomorphic mapping \(\Phi \colon V\to Y\) defined by the formula \(x\mapsto (f(x),g(x))\). The mapping \(\Phi \) extends to a meromorphic mapping from \(F\) to \(\bar Y\subset \PP ^2\), where \(\bar Y\) is the closure of \(Y\); composing this meromorphic mapping with a birational mapping \(\bar Y\dashrightarrow X\), one obtains a meromorphic mapping \(\Phi _1\colon F\dashrightarrow X\). Since, by our construction, \(\M (F)\cong \M (X)\), it suffices to show that \(X\cong \PP ^1\), or, equivalently, that there are no non-trivial holomorphic \(1\)-forms on \(X\).

To that end, let \(I\subset F\) be the indeterminacy locus of \(\Phi _1\); it is a discrete subset of \(F\). Choose a good neighborhood \(W\supset C\); since \(\Phi _1\) is not constant, there exists a non-empty open subset \(O\subset W\setminus I\) such that \(\rank D\Phi _1(x)=1\) for any \(x\in O\). Now if \(\omega \ne 0\) is a holomorphic form on \(X\), then \((\Phi _1|_{W\setminus I})^*\omega \) is a holomorphic form such that its restriction to \(O\) is not identically zero. Extending it to \(W\), one obtains a holomorphic \(1\)-form on \(W\) which is not identically zero. This contradicts Lemma  5.5 , and this contradiction completes the proof of Proposition  1.2 .